GUÍA No. 4

TERMODINÁMICA Y ELECTRICIDAD

¿Cómo entender las leyes de la termodinámica y las propiedades físicas de la materia para comprender su contribución en el diseño de máquinas que generan progreso y avance en la ciencia?

El desarrollo científico y tecnológico es una de los factores más influyentes  sobre la sociedad contemporánea.  La globalización mundial, polarizadora de la riqueza y el poder, sería impensable sin el avance de las fuerzas productivas que la ciencia y la tecnología han hecho posibles. La actividad tecnológica influye en el progreso social pero también en el deterioro de nuestro entorno. Actualmente la Tecnología está comprometida en conseguir procesos tecnológicos acordes con el medio ambiente, para evitar que las crecientes necesidades provoquen un agotamiento o degradación de los recursos materiales y energéticos de nuestro Planeta.

La termodinámica puede definirse como el tema de la Física que estudia los procesos en los que se transfiere energía como calor y como trabajo. Sabemos que se efectúa trabajo cuando la energía se transfiere de un cuerpo a otro por medios mecánicos. El calor es una transferencia de energía de un cuerpo a un segundo cuerpo que está a menor temperatura. O sea, el calor es muy semejante al trabajo.

Al hablar de termodinámica, con frecuencia se usa el término "sistema". Por sistema se entiende un objeto o conjunto de objetos que deseamos considerar. El resto, lo demás en el Universo, que no pertenece al sistema, se conoce como su "ambiente". Se consideran varios tipos de sistemas. En un sistema cerrado no entra ni sale masa, contrariamente a los sistemas abiertos donde sí puede entrar o salir masa. Un sistema cerrado es aislado si no pasa energía en cualquiera de sus formas por sus fronteras.

 

Primera Ley de la termodinámica

 Esta ley se expresa como:

Cambio en la energía interna en el sistema = Calor agregado (Q) - Trabajo efectuado por el sistema (W). Notar que el signo menos en el lado derecho de la ecuación se debe justamente a que W se define como el trabajo efectuado por el sistema.

Para entender esta ley, es útil imaginar un gas encerrado en un cilindro, una de cuyas tapas es un émbolo móvil y que mediante un mechero podemos agregarle calor. El cambio en la energía interna del gas estará dado por la diferencia entre el calor agregado y el trabajo que el gas hace al levantar el émbolo contra la presión atmosférica.

Segunda Ley de la Termodinámica

 La primera ley nos dice que la energía se conserva. Sin embargo, podemos imaginar muchos procesos en que se conserve la energía, pero que realmente no ocurren en la naturaleza. Si se acerca un objeto caliente a uno frío, el calor pasa del caliente al frío y nunca al revés. Si pensamos que puede ser al revés, se seguiría conservando la energía y se cumpliría la primera ley.

En la naturaleza hay procesos que suceden, pero cuyos procesos inversos no. Para explicar esta falta de reversibilidad se formuló la segunda ley de la termodinámica, que tiene dos enunciados equivalentes:

Enunciado de Kelvin - Planck: Es imposible construir una máquina térmica que, operando en un ciclo, no produzca otro efecto que la absorción de energía desde un depósito y la realización de una cantidad igual de trabajo.

Enunciado de Clausius: Es imposible construir una máquina cíclica cuyo único efecto sea la transferencia continua de energía de un objeto a otro de mayor temperatura sin la entrada de energía por trabajo.

Tercera Ley de la Termodinámica.

"No se puede llegar al cero absoluto mediante una serie finita de procesos". Es el calor que entra desde el "mundo exterior" lo que impide que en los experimentos se alcancen temperaturas más bajas. El cero absoluto es la temperatura teórica más baja posible y se caracteriza por la total ausencia de calor. Es la temperatura a la cual cesa el movimiento de las partículas. El cero absoluto (0 K) corresponde aproximadamente a la temperatura de - 273,16ºC. Nunca se ha alcanzado tal temperatura y la termodinámica asegura que es inalcanzable.

"La entropía de cualquier sustancia pura en equilibrio termodinámico tiende a cero a medida que la temperatura tiende a cero".

"La primera y la segunda ley de la termodinámica se pueden aplicar hasta el límite del cero absoluto, siempre y cuando en este límite las variaciones de entropía sean nulas para todo proceso reversible".

¿Cómo Comprender de manera activa y practica los campos electrostáticos y los INDICADORES avances en la producción de gran cantidad de dispositivos que han contribuido al desarrollo de la humanidad?

La ciencia y la tecnología han terminado por transformar numerosos espacios de las sociedades contemporáneas. Son innegables los beneficios que de tal transformación se obtienen, pero también son numerosos los riesgos que han surgido de tan vertiginoso desarrollo. Esta doble condición obliga a que la ciencia y la tecnología deban ser vistas con una actitud más crítica, ya que no siempre son los mismos impactos los que se presentan en el mundo desarrollado que en los países del sur.

Las cargas eléctricas no precisan de ningún medio material para influir entre ellas y por ello las fuerzas eléctricas son consideradas fuerzas de acción a distancia. En virtud de ello se recurre al concepto de campo electrostático para facilitar la descripción, en términos físicos, de la influencia que una o más cargas ejercen sobre el espacio que les rodea.

El concepto de campo surge ante la necesidad de explicar la forma de interacción entre cuerpos en ausencia de contacto físico y sin medios de sustentación para las posibles interacciones. La acción a distancia se explica, entonces, mediante efectos provocados por la entidad causante de la interacción, sobre el espacio mismo que la rodea, permitiendo asignar a dicho espacio propiedades medibles. Así, será posible hacer corresponder a cada punto del espacio valores que dependerán de la magnitud de la propiedad del cuerpo que provoca la interacción y de la ubicación del punto que se considera.

Ejemplos de fenómenos electroestáticos

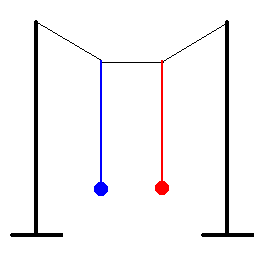
1.  Poniendo muy próximos dos péndulos eléctricos tocados con vidrio frotado, se observa una repulsión mutua; si los dos se han tocado con resina frotada, la repulsión se origina análogamente; si uno de los dos péndulos se ha puesto en contacto con resina frotada y el otro con vidrio, se produce una mutua atracción.

2.  Cuando frotamos una barra de vidrio con un paño. Lo que hemos hecho es arrancar cargas negativas de la barra que han quedado atrapadas en el paño, por lo que la barra inicialmente neutra ha quedado con defecto de cargas negativas (cargada positivamente) y el paño con un exceso de cargas negativas, en el sistema total vidrio-paño, la carga eléctrica no se ha modificado, únicamente se ha redistribuido.

3.  Cuando caminas por alfombra y tocas el pivote de la puerta metálico. Sientes una descarga eléctrica.

4.     Cuando te peinas con un peine puedes recoger pedacitos de papel con el peine.

Ahora bien, La mecánica es la rama de la física que estudia y analiza el movimiento y reposo de los cuerpos, y su evolución en el tiempo, bajo la acción de fuerzas. El conjunto de disciplinas que abarca la mecánica convencional es muy amplio y es posible agruparlas en cuatro bloques principales:

Mecánica clásica	Mecánica cuántica
Mecánica relativista	Teoría cuántica de campos

La mecánica es una ciencia perteneciente a la física, ya que los fenómenos que estudia son físicos, por ello está relacionada con las matemáticas. Sin embargo, también puede relacionarse con la ingeniería, en un modo menos riguroso. Ambos puntos de vista se justifican parcialmente ya que, si bien la mecánica es la base para la mayoría de las ciencias de la ingeniería clásica, no tiene un carácter tan empírico como éstas y, en cambio, por su rigor y razonamiento deductivo, se parece más a la matemática.

Mecánica clásica

La mecánica clásica está formada por áreas de estudio que van desde la mecánica del sólido rígido y otros sistemas mecánicos con un número finito de grados de libertad, como la mecánica de medios continuos (sistemas con infinitos grados de libertad). Existen dos formulaciones diferentes, que difieren en el grado de formalización para los sistemas con un número finito de grados de libertad:

Mecánica newtoniana. Dio origen a las demás disciplinas y se divide en varias de ellas: la cinemática, estudio del movimiento en sí, sin atender a las causas que lo originan; la estática, que estudia el equilibrio entre fuerzas y la dinámica que es el estudio del movimiento atendiendo a sus orígenes, las fuerzas.

Mecánica analítica, una formulación matemática muy potente de la mecánica newtoniana basada en el principio de Hamilton, que emplea el formalismo de variedades diferenciables, en concreto el espacio de configuración y el espacio fásico.

Mecánica estadística

La mecánica estadística trata de sistemas con muchas partículas y que por tanto tienen un número elevado de grados de libertad, al punto que no resulta posible escribir todas las ecuaciones de movimiento involucradas y, en su defecto, trata de resolver aspectos parciales del sistema por métodos estadísticos que dan información útil del comportamiento global del sistema sin especificar qué sucede con cada partícula del sistema. Los resultados obtenidos coinciden con los resultados de la termodinámica. Usa tanto formulaciones de la mecánica hamiltoniana como formulaciones de la teoría de probabilidad. Existen estudios de mecánica estadística basados tanto en la mecánica clásica como en la mecánica cuántica.

Mecánica relativista

La Mecánica relativista o Teoría de la Relatividad comprende:

• La Teoría de la Relatividad Especial, que describe adecuadamente el comportamiento clásico de los cuerpos que se mueven a grandes velocidades en un espacio-tiempo plano (no-curvado).
• La Teoría general de la relatividad, que generaliza la anterior describiendo el movimiento en espacios-tiempo curvados, además de englobar una teoría relativista de la gravitación que generaliza la teoría de la gravitación de Newton.

Existen varias propiedades interesantes de la dinámica relativista, entre ellas:

La fuerza y la aceleración no son en general vectores paralelos en una trayectoria curva, ya que la relación entre la aceleración y la fuerza tangenciales es diferente que la que existe entre la aceleración y fuerza normales. Tampoco la razón entre el módulo de la fuerza y el módulo de la aceleración es constante, ya que en ella aparece el inverso del factor de Lorentz, que es decreciente con la velocidad llegando a ser nulo a velocidades cercanas a la velocidad de la luz.

El intervalo de tiempo medido por diferentes observadores en movimiento relativo no coinicide, por lo que no existe un tiempo absoluto, y no puede establecerse un presente común a todos los observadores, aunque se mantienen relaciones de causalidad estrictas.

Otro hecho interesante de la mecánica relativista es que elimina la acción a distancia. Las fuerzas que experimenta una partícula en el campo gravitatorio o electromagnético provocado por otras partículas depende de la posición de las partículas en un instante anterior, siendo el "retraso" en la influencia que ejercen unas partículas sobre otras del orden de la distancia dividida entre la velocidad de la luz:

Sin embargo, a pesar de todas estas diferencias la mecánica relativista es mucho más similar a la mecánica clásica desde un punto de vista formal, que la mecánica cuántica. La mecánica relativista sigue siendo una teoría estrictamente determinista, por ejemplo.

Mecánica cuántica

La mecánica cuántica trata con sistemas mecánicos de pequeña escala o con energía muy pequeñas (y ocasionalmente sistemas macroscópicos que exhiben cuantización de alguna magnitud física). En esos casos los supuestos de la mecánica clásica no son adecuados. En particular el principio de determinación por el cual el estado futuro del sistema depende por completo del estado actual no parece ser válido, por lo que los sistemas pueden evolucionar en ciertos momentos de manera no determinista (ver postulado IV y colapso de la función de onda), ya que las ecuaciones para la función de onda de la mecánica cuántica no permiten predecir el estado del sistema después de una medida concreta, asunto conocido como problema de la medida. Sin embargo, el determinismo también está presente porque entre dos medidas filtrantes el sistema evoluciona de manera determinista de acuerdo con la ecuación de Schrödinger.

La evolución no determinista y las medidas sobre un sistema, están regidas por un enfoque probabilístico. En mecánica cuántica este enfoque probabilístico, lleva por ejemplo en el enfoque más común renunciar al concepto de trayectoria de una partícula. Peor aún el concepto la interpretación de Copenhague renuncia por completo a la idea de que las partículas ocupen un lugar concreto y determinado en el espacio-tiempo. La estructura interna de algunos sistemas físicos de interés como los átomos o las moléculas sólo pueden ser explicados mediante un tratamiento cuántico, ya que la mecánica clásica hace predicciones sobre dichos sistemas que contradicen la evidencia física. En ese sentido la mecánica cuántica se considera una teoría más exacta o más fundamental que la mecánica clásica que actualmente sólo se considera una simplificación conveniente de la mecánica cuántica para cuerpos macroscópicos.

También existe una mecánica estadística cuántica que incorpora restricciones cuánticas en el tratamiento de los agregados de partículas.

Mecánica cuántica relativista

La mecánica cuántica relativista trata de aunar mecánica relativista y mecánica cuántica, aunque el desarrollo de esta teoría lleva a la conclusión de que en un sistema cuántico relativista el número de partículas no se conserva y de hecho no puede hablarse de una mecánica de partículas, sino simplemente de una teoría cuántica de campos. Esta teoría logra aunar principios cuánticos y teoría de la relatividad especial (aunque no logra incorporar los principios de la relatividad general). Dentro de esta teoría, no se consideran ya estados de las partículas sino del espacio-tiempo. De hecho cada uno de los estados cuánticos posibles del espacio tiempo viene caracterizado por el número de partículas de cada tipo representadas por campos cuánticos y las propiedades de dichos campos.

Es decir, un universo donde existan Ni partículas del tipo i en los estados cuánticos 

E1, ..., ENi representa un estado cuántico diferente de otro estado en el que observamos en mismo universo con un número diferente de partículas. Pero ambos, "estados" o aspectos del universo son dos de los posibles estados cuánticos físicamente realizables del espacio-tiempo. De hecho la noción de partícula cuántica es abandonada en la teoría cuántica de campos, y esta noción se substituye por la de campo cuántico. Un campo cuántico es una aplicación que asigna a una función suave sobre una región del espacio-tiempo un operador auto adjunto. La función suave representa la región donde se mide el campo, y los valores propios del operador número asociado al campo el número de partículas observables a la hora de realizar una medida de dicho campo.