miércoles, 14 de marzo de 2012

MAQUINAS TERMICAS


Máquina térmica y motor térmico

Aunque en algunas definiciones se identifican como sinónimos los

términos «máquina térmica motora» y «motor térmico», en otras se

diferencian ambos conceptos. Al diferenciarlos, se considera que un

motor térmico es un conjunto de elementos mecánicos que permite

obtener energía mecánica a partir de la energía térmica obtenida

mediante una reacción de combustión o una reacción nuclear. Un

motor térmico dispone de lo necesario para obtener energía térmica,

mientras que una máquina térmica motora necesita energía térmica

para funcionar, mediante un fluido que dispone de más energía a la

entrada que a la salida.[1]

Clasificación             

Según el sentido de transferencia de energía

Las máquinas térmicas pueden clasificarse, según el sentido de transferencia de energía, en:

• Máquinas térmicas motoras, en las cuales la energía del fluido disminuye al atravesar la máquina, obteniéndose

energía mecánica en el eje.

Máquina térmica 2

Un compresor de émbolos usado en un ciclo de

refrigeración.

Compresor rotodinámico axial.

Compresor rotodinámico centrífugo y su

triángulo de velocidades a la salida.

• Máquinas térmicas generadoras, en las cuales la energía del fluido.
aumenta al atravesar la máquina, precisándose energía mecánica en
el eje.

Según el principio de funcionamiento

Atendiendo al principio de funcionamiento, las máquinas térmicas se

clasifican en:

• Máquinas volumétricas o máquinas de desplazamiento positivo,

cuyo funcionamiento está basado en principios mecánicos e

hidrostáticos, de manera que el fluido en algún instante está

contenido en un volumen limitado por los elementos de la máquina.

En este tipo de máquinas el flujo es pulsatorio. Se dividen a su vez

en dos tipos según el movimiento del órgano propulsor: altenativas,

cuyo movimiento es rectilíneo; y rotativas, cuyo movimiento es

circular.

• Turbomáquinas, cuyo funcionamiento está basado en el intercambio

de cantidad de movimiento entre el fluido y un rodete. En estas

máquinas el flujo es continuo.

Teniendo en cuenta lo anterior, podemos clasificar las máquinas

térmicas tal como se recoge en el cuadro siguiente.


Clasificación
Según el sentido de transferencia de energía
Las máquinas térmicas pueden clasificarse, según el sentido de transferencia de energía, en:
• Máquinas térmicas motoras, en las cuales la energía del fluido disminuye al atravesar la máquina, obteniéndose
energía mecánica en el eje.    
Máquina térmica 2
File:Compresor alternativo R22.jpg
Un compresor de émbolos usado en un ciclo de
refrigeración.
Compresor rotodinámico axial.
Compresor rotodinámico centrífugo y su
triángulo de velocidades a la salida.
• Máquinas térmicas generadoras, en las cuales la energía del fluido
aumenta al atravesar la máquina, precisándose energía mecánica en
el eje.
Lysholm_screw_rotors.jpg‎ (500 × 506 pixels, file size: 35 KB, MIME type: image/jpeg)
DescriptionLysholm screw rotors. I created this for the supercharger article
Date2006-06-17 (first version); 2006-06-17 (last version)
SourceOriginally from en.wikipedia; description page is/was here.
AuthorOriginal uploader was Motorhead at en.wikipedia
Permission
(Reusing this file)

Según el principio de funcionamiento
Atendiendo al principio de funcionamiento, las máquinas térmicas se
clasifican en:
• Máquinas volumétricas o máquinas de desplazamiento positivo,
cuyo funcionamiento está basado en principios mecánicos e
hidrostáticos, de manera que el fluido en algún instante está
contenido en un volumen limitado por los elementos de la máquina.
En este tipo de máquinas el flujo es pulsatorio. Se dividen a su vez
en dos tipos según el movimiento del órgano propulsor: altenativas,
cuyo movimiento es rectilíneo; y rotativas, cuyo movimiento es
circular.
• Turbomáquinas, cuyo funcionamiento está basado en el intercambio
de cantidad de movimiento entre el fluido y un rodete. En estas
máquinas el flujo es continuo.
Teniendo en cuenta lo anterior, podemos clasificar las máquinas
Máquinas térmicas
MotorasVolumétricasAlternativasMáquina de vapor
RotativasMotor Stirling
TurbomáquinasTurbina
GeneradorasVolumétricasAlternativasCompresor de émbolo
RotativasCompresor rotativo
TurbomáquinasTurbocompresor



 
Balance de energía en una máquina térmica
Un sistema abierto es aquel que intercambia materia y energía con el entorno. Aplicando el primer principio de la termodinámica para un sistema abierto, el incremento de energía del sistema en un intervalo de tiempo es:
\Delta E_{sistema} = Q + W + \sum_{in} m_{in} (h + \frac1 2 V^{2} + gz)_{in}-\sum_{out} m_{out} (h + \frac1 2 V^{2} + gz)_{out}

 donde;
    Q es el calor entregado al sistema. Será negativo cuando el calor sea entregado por el sistema.
  • W es el trabajo entregado al sistema, en forma de trabajo mecánico y energía de presión. Será negativo cuando el calor sea entregado por el sistema.
  • El subíndice in representa la materia que entra al sistema.
  • El subíndice out representa la materia que sale del sistema.
  • h es la entalpía por unidad de masa del flujo
  • V2/2 es la energía cinética por unidad de masa del flujo.
  • gz es la energía potencial por unidad de masa del flujo
Haciendo la derivada de la expresión anterior respecto al tiempo, se obtiene:\frac{dE_{sistema}}{dt} = \dot Q + \dot W + \dot m_{in} (h + \frac1 2 V^{2} + gz)_{in}- \dot m_{out} (h + \frac1 2 V^{2} + gz)_{out}
Debe tenerse en cuenta que en máquinas generadoras, puede aparecer esta expresión con el signo de W cambiado, para que se exprese el trabajo entregado por la máquina y así W sea positivo.
Véase también: Criterio de signos termodinámico
Simplificaciones
La ecuación que expresa el balance de energía puede simplificarse en los siguientes casos:
Sistema en reposo
Cuando el sistema está en reposo, tal como en máquinas estacionarias, las variaciones de energía potencial y energía cinética serán nulas.
\frac {dE_{sistema}}{dt} = \frac{dU}{dt} + \frac{E_c}{dt} + \frac{E_p}{dt} = \frac{dU}{dt}
Régimen permanente
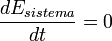
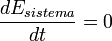
Cuando la máquina funciona en régimen permanente, las cantidades de masa y energía que entran son iguales a las que salen, pues de lo contrario variarían esa cantidades dentro del sistema.\frac {dE_{sistema}}{dt} = 0

Variación de energía potencial despreciable
En la mayoría de las máquinas térmicas, diferencia de energía potencial del flujo que sale respecto al que entra es poco significativo en comparación con los otros términos asociados a la energía del flujo.
\Delta (gz) \ll \Delta \left (h + \frac1 2 V^{2} \right ) \Rightarrow \Delta (gz) \approx 0
Sistemas adiabáticos
En la mayoría de las máquinas térmicas, la transferencia de calor es despreciable frente a otros intercambios de energía. Teniendo en cuenta la transmisión de calor por conducción y convección:\dot Q = \frac{dQ}{dt} = U \cdot A \cdot \Delta T_{LM} \approx 0
donde Q es el calor intercambiado, U es el coeficiente global de transferencia de calor, A es la superficie del sistema y es la diferencia de temperaturas media logarítmica, puede considerarse que el sistema es adiabático cuando se da alguna de las siguientes condiciones:
  • La superficie externa del sistema está bien aislada térmicamente.
  • La superficie externa del sistema es muy pequeña.
  • La diferencia de temperaturas entre el flujo y el entorno del sistema es pequeña.
  • El fluido pasa a través de la máquina tan rápido que apenas hay tiempo para que sea significativa la transferencia de calor por unidad de masa.
 Máquina térmica en régimen permanente con variación de energía potencial despreciable
En una máquina térmica que funciona en régimen permanente en la cual se desprecie la variación de energía potencial, la expresión el primer principio de la termodinámica puede expresarse como\dot W = \dot m [(h + \frac{V^{2}}{2})_{out} - (h + \frac{V^{2}}{2})_{in}] = \dot m [ h_{0 out} - h_{0 in} ]

donde es la entalpía de parada.
En los ciclos termodinámicos asociados a la turbina de vapor, la energía cinética específica puede considerarse despreciable frente a la entalpía, resultando\dot W = \dot m [(h + \frac{V^{2}}{2})_{out} - (h + \frac{V^{2}}{2})_{in}] = \dot m [ h_{0 out} - h_{0 in} ]
RendimientoDiagrama h-S de vapor de agua, en el que se muestran en rojo dos expansiones entre dos isobaras distintas. La presión de salida es una condición de contorno para el proceso. Con una expansión isoentrópica entre las presiones de entrada y de salida se obtendría mayor salto entálpico.
Para el cálculo del rendimiento, se relaciona la energía obtenida, ya sea en forma de incremento de energía en el fluido o de energía mecánica suministrada por la máquina, entre la máxima energía que se podría obtener en las condiciones de contorno.
 Rendimiento de una máquina térmica motora
Rendimiento interno
El trabajo específico máximo que puede obtenerse en la expansión de un fluido está definido por la diferencia de entalpías entre el fluido a la entrada y las condiciones isoentrópicas a la presión de salida. En cambio el trabajo real es menor a éste debido al aumento de la entropía.[2]\eta_i = \frac {\dot W_i}{\dot W_{max}} = \frac {\dot m (h_{01}-h_{02})}{\dot m (h_{01}-h_{02s})} = \frac {h_{01}-h_{02}}{h_{01}-h_{02s}}

Rendimiento mecánico
El rendimiento mecánico es la relación entre potencia efectiva (( ), que es la potencia obtenida en el eje, y la potencia interna (( ), que es la variación por unidad de tiempo de la energía del fluido. La potencia efectiva resulta de restar a la potencia indicada menos la potencia de pérdidas mecánicas ( ), que es disipada el rozamiento de elementos mecánicos (cojinetes, retenes, etc.) y en el accionamiento de elementos auxiliares (bomba de aceite, ventiladores, etc.    
)\eta_m = \frac {\dot W_e}{\dot W_i} = \frac {\dot W_i - \dot W_{pm}}{\dot W_i} = 1 - \frac {\dot W_{pm}}{\dot W_i}

Rendimiento isoentrópico
El rendimiento isoentrópico relaciona la potencia obtenida en el eje con potencia máxima del proceso isoentrópico en las mismas condiciones de contorno.
\eta_s = \frac {\dot W_e}{\dot W_{max}} = \frac {\dot W_e}{h_{01}-h_{02s}}
 Rendimiento de una máquina térmica generadora
Rendimiento interno
El trabajo específico mínimo para comprimir un fluido desde un estado térmico hasta una presión determinada es igual al salto entálpico del correspondiente proceso isoentrópico, de forma que un proceso real presentará mayor diferencia de entalpías del fluido entre la entrada y la salida.[3
\eta_i = \frac {\dot W_{min}}{\dot W_i} = \frac {\dot m (h_{02s}-h_{01})}{\dot m (h_{02}-h_{01})} = \frac {h_{02s}-h_{01}}{h_{02}-h_{01}}

Rendimiento mecánico
El rendimiento mecánico es la relación entre potencia efectiva (( ), que es la potencia obtenida en el eje, y la potencia interna (( ), que es la variación por unidad de tiempo de la energía del fluido. La potencia efectiva resulta de restar a la potencia indicada menos la potencia de pérdidas mecánicas ( ), que es disipada el rozamiento de elementos mecánicos (cojinetes, retenes, etc.) y en el accionamiento de elementos auxiliares (bomba de aceite, ventiladores, etc.)  
  \eta_m = \frac {\dot W_i}{\dot W_e} = \frac {\dot W_e - \dot W_{pm}}{\dot W_e} = 1 - \frac {\dot W_{pm}}{\dot W_e}
Rendimiento isoentrópico
El rendimiento isoentrópico relaciona potencia mínima del proceso isoentrópico en las mismas condiciones de contorno con la potencia suministrada en el eje
.\eta_s = \frac {\dot W_{min}}{\dot W_e} = \frac {\dot m (h_{01s}-h_{01})}{\dot W_e}





Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)